1. Введение

Когда мы говорим о станках с ЧПУ, мы обычно думаем о станках, которым указано перемещаться в определенные места и выполнять различные задачи. Чтобы иметь единое представление о пространстве станка и соответствовать человеческой точке зрения в трехмерном пространстве, большинство станков (если не все) используют общую систему координат, называемую декартовой системой координат.

Декартова система координат состоит из трех осей (X, Y, Z), каждая из которых перпендикулярна двум другим footnote: [Слово "оси" также часто (и ошибочно) используется, когда речь идет о станках с ЧПУ и относится к направлениям движения станка.].

When we talk about a G-code program (RS274/NGC) we talk about a number of commands (G0, G1, etc.) which have positions as parameters (X- Y- Z-). These positions refer exactly to Cartesian positions. Part of the LinuxCNC motion controller is responsible for translating those positions into positions which correspond to the machine kinematics
[Kinematics: a two way function to transform from Cartesian space to joint space.]
.

1.1. Сочленения против осей

Сочленение станка с ЧПУ является одной из физических степеней свободы станка. Оно может быть линейное (ШВП) или вращательное (поворотные столы, сочленения манипуляторов робота). На одном станке может быть любое количество сочленений. Например, у одного популярного робота 6 сочленений, а у типичного простого фрезерного станка — всего 3.

There are certain machines where the joints are laid out to match kinematics axes (joint 0 along axis X, joint 1 along axis Y, joint 2 along axis Z), and these machines are called Cartesian machines (or machines with Trivial Kinematics). These are the most common machines used in milling, but are not very common in other domains of machine control (e.g. welding: puma-typed robots).

LinuxCNC поддерживает оси с именами: X Y Z A B C U V W. Оси X Y Z обычно относятся к обычным декартовым координатам. Оси A B C относятся к координатам вращения относительно осей X Y Z соответственно. Оси U V W относятся к дополнительным координатам, которые обычно коллинеарны осям X Y Z соответственно.

2. Тривиальная кинематика

Простейшими станкаи являются станки, в которых каждое сочленение расположено вдоль одной из декартовых осей. На этих станках отображение декартова пространства (программы G-кода) в пространство сочленения (реальные исполнительные механизмы станка) тривиально. Это простое сопоставление 1:1:

pos->tran.x = joints[0];
pos->tran.y = joints[1];
pos->tran.z = joints[2];

В приведенном выше фрагменте кода можно увидеть, как выполняется отображение: позиция X идентична сочленению 0, позиция Y — сочленению 1 и т. д. Вышеупомянутое относится к прямой кинематике (одно направление преобразования). Следующий фрагмент кода относится к обратной кинематике (или обратному направлению преобразования):

joints[0] = pos->tran.x;
joints[1] = pos->tran.y;
joints[2] = pos->tran.z;

В LinuxCNC тождественная кинематика реализована с помощью модуля кинематики trivkins и расширена до 9 осей. Соотношения по умолчанию между координатами осей и номерами сочленений следующие: footnote: [Если на станке (например, токарном станке) установлены только оси X, Z и A, а INI-файл LinuxCNC содержит только определения этих трех сочленений, то предыдущее утверждение неверно. Потому что в настоящее время у нас есть (joint0=X, Joint1=Z, Joint2=A), что предполагает, что Joint1=Y. Чтобы это работало в LinuxCNC, просто определите все оси (XYZA), LinuxCNC затем будет использовать простой цикл в HAL для неиспользуемой оси Y.] footnote: [Другой способ заставить это работать — изменить соответствующий код и перекомпилировать программное обеспечение. ]

pos->tran.x = joints[0];
pos->tran.y = joints[1];
pos->tran.z = joints[2];
pos->a      = joints[3];
pos->b      = joints[4];
pos->c      = joints[5];
pos->u      = joints[6];
pos->v      = joints[7];
pos->w      = joints[8];

Аналогичным образом, отношения по умолчанию для обратной кинематики для trivkins таковы:

joints[0] = pos->tran.x;
joints[1] = pos->tran.y;
joints[2] = pos->tran.z;
joints[3] = pos->a;
joints[4] = pos->b;
joints[5] = pos->c;
joints[6] = pos->u;
joints[7] = pos->v;
joints[8] = pos->w;

Преобразование для тривиальной "кинематики" (кинематика trivkins) или декартового станка выполнить несложно при условии, что в используемых буквах осей нет пропусков.

Ситуация становится немного сложнее, если на станке отсутствует одна или несколько букв оси. Проблемы с пропущенными буквами осей решаются с помощью параметра модуля coordinates= с модулем trivkins. Номера сочленений присваиваются последовательно каждой указанной координате. Токарный станок можно описать с помощью coordinates=xz. Тогда назначения сочленения будут следующими:

joints[0] = pos->tran.x
joints[1] = pos->tran.z

Использование параметра coordinates= рекомендуется для конфигураций, в которых отсутствуют буквы оси.
[ Исторически модуль trivkins не поддерживал параметр coordinates=, поэтому конфигурации токарных станков часто настраивались как станки XYZ. Неиспользуемая ось Y была настроена на 1) немедленное возвращение в исходное положение, 2) использование простой обратной связи для подключения контакта HAL команды положения к контакту HAL обратной связи по положению и 3) скрытие на ГИП дисплеев . Многие конфигурации SIM используют эти методы для совместного использования общих файлов HAL.]

Модуль кинематики trivkins также позволяет указывать одну и ту же координату для более чем одного сочленения. Эта функция может быть полезна на таких станках, как портальные, с двумя независимыми двигателями для координаты Y. Такой станок может использовать coordinates=xyyz, что приведет к назначеням сочленения:

joints[0] = pos->tran.x
joints[1] = pos->tran.y
joints[2] = pos->tran.y
joints[3] = pos->tran.z

Дополнительную информацию смотрите на страницах руководства trivkins.

3. Нетривиальная кинематика

Типов настроек станков может быть довольно много (роботы: пума, скара; гексаподы и т. д.). Каждый из них настраивается с помощью линейных и поворотных сочленений. Эти сочленения обычно не совпадают с декартовыми координатами, поэтому нам нужна кинематическая функция, которая выполняет преобразование (фактически две функции: прямая и обратная кинематика).

Для иллюстрации вышеизложенного разберем простую кинематику, называемую бипод (упрощенный вариант трипода, представляющий собой упрощенный вариант гексапода).

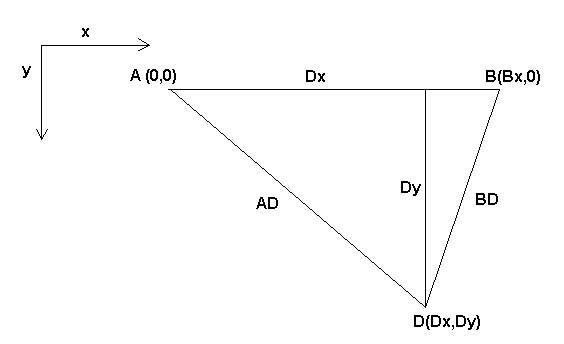
Настройка бипода
Figure 1. Настройка бипода

Бипод, о котором мы говорим, представляет собой устройство, состоящее из двух двигателей, размещенных на стене, к которой устройство подвешивается с помощью проволоки. Сочленениями в данном случае являются расстояния от двигателей до устройства (на рисунке обозначены AD и BD).

Положение двигателей фиксировано по соглашению. Двигатель A находится в (0,0), что означает, что его координата X равна 0, а его координата Y также равна 0. Двигатель B помещен в (Bx, 0), что означает, что его координата X равна Bx.

Наша режущая кромка инструмента будет находиться в точке D, которая определяется расстояниями AD и BD, а также декартовыми координатами Dx, Dy.

Задача кинематики заключается в преобразовании длин соединений (AD, BD) в декартовы координаты (Dx, Dy) и наоборот.

3.1. Forward transformation

Для преобразования из пространства сочленения в декартово пространство мы воспользуемся некоторыми правилами тригонометрии (прямоугольные треугольники, определяемые точками (0,0), (Dx,0), (Dx,Dy) и треугольник (Dx,0), (Bx ,0) и (Dx,Dy)).

Мы легко можем это увидеть:

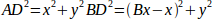
images/kinematics-math-01.png

так же:

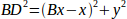
images/kinematics-math-02.png

Если вычесть одно из другого, то получим:

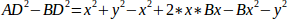
images/kinematics-math-03.png

и поэтому:

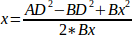
images/kinematics-math-04.png

и поэтому:

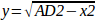
images/kinematics-math-05.png

Обратите внимание, что вычисление y включает квадратный корень из разницы, что может не привести к действительному числу. Если для этого совместного положения не существует единой декартовой координаты, то такое положение называется особенностью. В этом случае прямая кинематика возвращает -1.

Переведено на реальный код:

double AD2 = joints[0] * joints[0];
double BD2 = joints[1] * joints[1];
double x = (AD2 - BD2 + Bx * Bx) / (2 * Bx);
double y2 = AD2 - x * x;
if(y2 < 0) return -1;
pos->tran.x = x;
pos->tran.y = sqrt(y2);
return 0;

3.2. Обратное преобразование

Обратная кинематика в нашем примере намного проще, так как мы можем записать ее непосредственно:

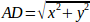
images/kinematics-math-06.png
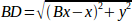
images/kinematics-math-07.png

или переведено в реальный код:

double x2 = pos->tran.x * pos->tran.x;
double y2 = pos->tran.y * pos->tran.y;
joints[0] = sqrt(x2 + y2);
joints[1] = sqrt((Bx - pos->tran.x)*(Bx - pos->tran.x) + y2);
return 0;

4. Детали реализации

Модуль кинематики реализован как компонент HAL и может экспортировать контакты и параметры. Он состоит из нескольких функций "C" (в отличие от функций HAL):

int kinematicsForward(const double *joint, EmcPose *world,
const KINEMATICS_FORWARD_FLAGS *fflags,
KINEMATICS_INVERSE_FLAGS *iflags)

Реализует forward kinematics function.

int kinematicsInverse(const EmcPose * world, double *joints,
const KINEMATICS_INVERSE_FLAGS *iflags,
KINEMATICS_FORWARD_FLAGS *fflags)

Реализует функцию обратной кинематики.

KINEMATICS_TYPE kinematicsType(void)

Возвращает идентификатор типа кинематики, например KINEMATICS_BOTH:

  1. KINEMATICS_IDENTITY (каждый номер сочленения соответствует букве оси)

  2. KINEMATICS_BOTH (forward and inverse kinematics functions are provided)

  3. KINEMATICS_FORWARD_ONLY

  4. KINEMATICS_INVERSE_ONLY

Note
 ГИПы могут интерпретировать KINEMATICS_IDENTITY, чтобы скрыть различия между номерами сочленений и буквами осей в режиме сочленения (обычно до возврата в исходное положение). 
int kinematicsSwitchable(void)
int kinematicsSwitch(int switchkins_type)
KINS_NOT_SWITCHABLE

Функция kinematicsSwitchable() возвращает 1, если поддерживается несколько типов кинематики. Функция kinematicsSwitch() выбирает тип кинематики. См. Switchable Kinematitcs.

Note
 Большинство предоставляемых модулей кинематики поддерживают один тип кинематики и используют директиву "KINS_NOT_SWITCHABLE" для предоставления значений по умолчанию для необходимых функций kinematicsSwitchable() и kinematicsSwitch(). 
int kinematicsHome(EmcPose *world, double *joint,
KINEMATICS_FORWARD_FLAGS *fflags,
KINEMATICS_INVERSE_FLAGS *iflags)

Функция кинематики исходного положения устанавливает для всех своих аргументов правильные значения в известной исходной позиции. При вызове им следует установить, если они известны, начальные значения, например, из INI-файла. Если кинематика исходного положения допускает произвольные начальные точки, следует использовать эти начальные значения.

int rtapi_app_main(void)
void rtapi_app_exit(void)

Это стандартные функции настройки и разборки модулей RTAPI.

Если модули кинематики содержатся в одном исходном файле, их можно скомпилировать и установить с помощью команды halcompile. Дополнительную информацию смотрите на странице руководства halcompile(1) или в руководстве по HAL.

4.1. Модуль кинематики с использованием шаблона userkins.comp

Другой способ создать собственный модуль кинематики — адаптировать userkins компонента HAL. Этот компонент шаблона может быть изменен пользователем локально и может быть создан с помощью halcompile.

Дополнительную информацию см. на страницах руководства пользователя userkins.

Отметим, что для создания переключаемых кинематических модулей необходимые доработки несколько сложнее.

См. millturn.comp как пример переключаемого кинематического модуля, созданного с использованием шаблона userkins.comp.