1. Einführung

Wenn wir über CNC-Maschinen sprechen, denken wir in der Regel an Maschinen, die angewiesen werden, sich an bestimmte Orte zu bewegen und verschiedene Aufgaben auszuführen. Um eine einheitliche Sicht auf den Maschinenraum zu haben und ihn an die menschliche Sichtweise im 3D-Raum anzupassen, verwenden die meisten Maschinen (wenn nicht alle) ein gemeinsames Koordinatensystem, das kartesische Koordinatensystem.

Das kartesische Koordinatensystem besteht aus drei Achsen (X, Y, Z), die jeweils senkrecht zueinander stehen. footnote: [Das Wort "Achsen" wird auch häufig (und fälschlicherweise) verwendet, wenn von CNC-Maschinen die Rede ist, und bezieht sich auf die Bewegungsrichtungen der Maschine.].

Wenn wir über ein G-Code-Programm (RS274/NGC) sprechen, dann meist über eine Reihe von Befehlen (G0, G1 usw.), die Positionen als Parameter haben (X- Y- Z-). Diese Positionen beziehen sich genau auf kartesische Positionen. Ein Teil der LinuxCNC Motion Controller ist verantwortlich für die Übersetzung dieser Positionen in Maschinen-Positionen und deren Kinematik entsprechen
[Kinematik: eine Zwei-Wege-Funktion, um aus dem kartesischen Raum in den Gelenkraum zu transformieren.]
.

1.1. Gelenke(engl. joints) vs. Achsen (engl. axes)

Ein Gelenk einer CNC-Maschine ist einer der physikalischen Freiheitsgrade der Maschine. Dies kann linear (Spindeln) oder rotierend (Drehtische, Roboterarmgelenke) sein. Es kann eine beliebige Anzahl von Gelenken an einer bestimmten Maschine geben. Ein beliebter Roboter hat beispielsweise 6 Gelenke, während eine typische einfache Fräsmaschine nur 3 hat.

Es gibt bestimmte Maschinen, bei denen die Gelenke so angeordnet sind, dass sie mit den kinematischen Achsen übereinstimmen (Gelenk 0 entlang der X-Achse, Gelenk 1 entlang der Y-Achse, Gelenk 2 entlang der Z-Achse); diese Maschinen nennt man Kartesische Maschinen (oder Maschinen mit Trivialkinematik). Diese Maschinen werden am häufigsten beim Fräsen verwendet, sind aber in anderen Bereichen der Maschinensteuerung (z. B. Schweißen: puma-typische Roboter) nicht sehr verbreitet.

LinuxCNC unterstützt Achsen mit Namen: X Y Z A B C U V W. Die X Y Z-Achsen beziehen sich normalerweise auf die üblichen kartesischen Koordinaten. Die A B C Achsen beziehen sich auf Rotationskoordinaten um die X Y Z Achsen. Die Achsen U V W beziehen sich auf zusätzliche Koordinaten, die üblicherweise kolinear zu den X-Y-Z-Achsen angeordnet sind.

2. Triviale Kinematik

Die einfachsten Maschinen sind solche, bei denen jedes Gelenk entlang einer der kartesischen Achsen angeordnet ist. Bei diesen Maschinen ist die Abbildung vom kartesischen Raum (das G-Code-Programm) auf den Gelenkraum (die tatsächlichen Aktoren der Maschine) trivial. Es handelt sich um eine einfache 1:1-Abbildung:

pos->tran.x = joints[0];
pos->tran.y = joints[1];
pos->tran.z = joints[2];

Im obigen Codeschnipsel kann man sehen, wie die Zuordnung erfolgt: die X-Position ist identisch mit dem Gelenk 0, die Y-Position mit dem Gelenk 1 usw. Die obige Darstellung bezieht sich auf die direkte Kinematik (eine Richtung der Transformation). Der nächste Codeschnipsel bezieht sich auf die inverse Kinematik (oder die umgekehrte Richtung der Transformation):

joints[0] = pos->tran.x;
joints[1] = pos->tran.y;
joints[2] = pos->tran.z;

In LinuxCNC wird die Identitätskinematik mit dem Kinematikmodul "trivkins" implementiert und auf 9 Achsen erweitert. Die Standardbeziehungen zwischen Achsenkoordinaten und Gelenknummern sind:
[Wenn die Maschine (z. B. eine Drehmaschine) nur mit den X-, Z- und A-Achsen gemountet ist und die INI-Datei von LinuxCNC nur die Definition dieser 3 Verbindungen enthält, ist die vorherige Behauptung falsch. Weil wir derzeit haben (Gelenk0 = X, Gelenk 1 = Z, Gelenk 2 = A), die davon ausgeht, dass Gelenk 1 = Y. Um dies in LinuxCNC zum Laufen zu bringen, definieren Sie einfach alle Achsen (XYZA), LinuxCNC verwendet dann eine einfache Schleife in HAL für nicht verwendete Y-Achse.]
 Fußnote:[Eine andere Möglichkeit, es zum Laufen zu bringen, besteht darin, den entsprechenden Code zu ändern und die Software neu zu kompilieren.]

pos->tran.x = joints[0];
pos->tran.y = joints[1];
pos->tran.z = joints[2];
pos->a      = joints[3];
pos->b      = joints[4];
pos->c      = joints[5];
pos->u      = joints[6];
pos->v      = joints[7];
pos->w      = joints[8];

Ähnlich sind die Standardbeziehungen für die inverse Kinematik für trivkins:

joints[0] = pos->tran.x;
joints[1] = pos->tran.y;
joints[2] = pos->tran.z;
joints[3] = pos->a;
joints[4] = pos->b;
joints[5] = pos->c;
joints[6] = pos->u;
joints[7] = pos->v;
joints[8] = pos->w;

Die Umwandlung für eine triviale "kins"-Kinematik oder eine kartesische Maschine ist einfach zu bewerkstelligen, sofern die verwendeten Achsenbuchstaben keine Lücken aufweisen.

Etwas komplizierter wird es, wenn der Maschine ein oder mehrere Achsenbuchstaben fehlen. Das Problem der fehlenden Achsenbuchstaben wird durch die Verwendung des Modulparameters coordinates= mit dem Modul trivkins gelöst. Jeder angegebenen Koordinate werden fortlaufend Gelenknummern zugewiesen. Eine Drehmaschine kann mit coordinates=xz beschrieben werden. Die Gelenkzuweisungen lauten dann:

joints[0] = pos->tran.x
joints[1] = pos->tran.z

Die Verwendung des Parameters coordinates= wird für Konfigurationen empfohlen, bei denen die Achsenbuchstaben weggelassen werden. Fußnote:[ In der Vergangenheit unterstützte das Modul trivkins den Parameter coordinates= nicht, so dass Drehmaschinen-Konfigurationen oft als XYZ-Maschinen konfiguriert wurden. Die unbenutzte Y-Achse wurde so konfiguriert, dass sie 1) sofort in die Ausgangsposition fährt, 2) einen einfachen Loopback verwendet, um ihren Positionsbefehls-HAL-Pin mit ihrem Positionsrückmeldungs-HAL-Pin zu verbinden, und 3) in der Benutzeroberfläche nicht angezeigt wird. Zahlreiche Sim-Konfigurationen verwenden diese Methoden, um gemeinsame HAL-Dateien zu nutzen.]

Das Kinematikmodul trivkins erlaubt es auch, dieselbe Koordinate für mehr als ein Gelenk anzugeben. Diese Funktion kann bei Maschinen wie einem Portal mit zwei unabhängigen Motoren für die y-Koordinate nützlich sein. Eine solche Maschine könnte coordinates=xyyz verwenden, was zu Gelenkzuweisungen führt:

joints[0] = pos->tran.x
joints[1] = pos->tran.y
joints[2] = pos->tran.y
joints[3] = pos->tran.z

Weitere Informationen finden Sie auf den Manpages von trivkins.

3. Nicht-triviale Kinematik

Es gibt verschiedene Arten von Maschinenaufbauten (Roboter: Puma, Scara, Hexapods usw.). Jeder von ihnen ist mit linearen und rotierenden Gelenken ausgestattet. Diese Gelenke stimmen in der Regel nicht mit den kartesischen Koordinaten überein, daher benötigen wir eine Kinematikfunktion, welche die Umrechnung vornimmt (eigentlich 2 Funktionen: Vorwärts- und Rückwärtskinematikfunktion).

Zur Veranschaulichung der obigen Ausführungen werden wir eine einfache Kinematik namens Zweibein (eine vereinfachte Version des Dreibeins, das eine vereinfachte Version des Hexapods ist) analysieren.

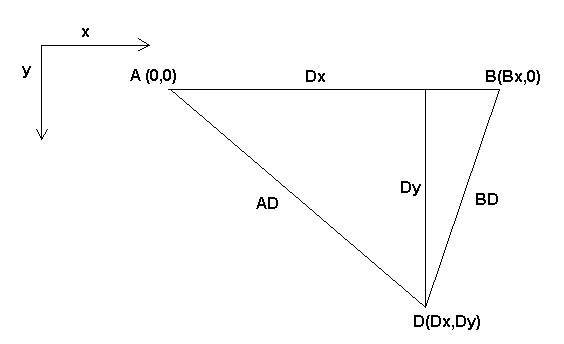
Zweibein-Einrichtung
Abbildung 1. Zweibein-Einrichtung

Das Zweibein (engl. bipod), um das es hier geht, besteht aus zwei Motoren, die an einer Wand angebracht sind und an denen ein Gerät mit einem Draht aufgehängt ist. Die Gelenke sind in diesem Fall die Abstände zwischen den Motoren und dem Gerät (in der Abbildung mit AD und BD bezeichnet).

Die Position der Motoren ist per Konvention festgelegt. Motor A befindet sich in (0,0), was bedeutet, dass seine X-Koordinate 0 und seine Y-Koordinate ebenfalls 0 ist. Motor B befindet sich in (Bx, 0), was bedeutet, dass seine X-Koordinate Bx ist.

Unser Tooltip befindet sich im Punkt D, der durch die Abstände AD und BD und die kartesischen Koordinaten Dx, Dy definiert wird.

Die Aufgabe der Kinematik besteht darin, die Gelenklängen (AD, BD) in kartesische Koordinaten (Dx, Dy) und umgekehrt zu transformieren.

3.1. Vorwärts-Transformation

Um vom gemeinsamen Raum in den kartesischen Raum zu transformieren, werden wir einige trigonometrische Regeln anwenden (die rechtwinkligen Dreiecke, die durch die Punkte (0,0), (Dx,0), (Dx,Dy) und das Dreieck (Dx,0), (Bx,0) und (Dx,Dy) bestimmt werden).

Wir können leicht erkennen, dass:

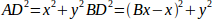
images/kinematics-math-01.png

ebenso:

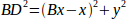
images/kinematics-math-02.png

Wenn wir das eine von dem anderen abziehen, erhalten wir:

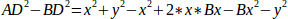
images/kinematics-math-03.png

und deshalb:

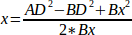
images/kinematics-math-04.png

Daraus berechnen wir:

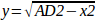
images/kinematics-math-05.png

Beachten Sie, dass die Berechnung von y die Quadratwurzel aus einer Differenz beinhaltet, was nicht unbedingt eine reelle Zahl ergibt. Wenn es keine einzige kartesische Koordinate für diese Gelenkposition gibt, dann wird die Position als Singularität bezeichnet. In diesem Fall liefert die Vorwärtskinematik den Wert -1.

Übersetzt in den tatsächlichen Code:

double AD2 = joints[0] * joints[0];
double BD2 = joints[1] * joints[1];
double x = (AD2 - BD2 + Bx * Bx) / (2 * Bx);
double y2 = AD2 - x * x;
if(y2 < 0) return -1;
pos->tran.x = x;
pos->tran.y = sqrt(y2);
return 0;

3.2. Inverse Transformation

Die inverse Kinematik ist in unserem Beispiel viel einfacher, da wir sie direkt schreiben können:

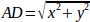
images/kinematics-math-06.png
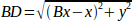
images/kinematics-math-07.png

oder in tatsächlichen Code übersetzt:

double x2 = pos->tran.x * pos->tran.x;
double y2 = pos->tran.y * pos->tran.y;
joints[0] = sqrt(x2 + y2);
joints[1] = sqrt((Bx - pos->tran.x)*(Bx - pos->tran.x) + y2);
return 0;

4. Details zur Implementierung

Ein Kinematikmodul ist als HAL-Komponente implementiert und darf Pins und Parameter exportieren. Es besteht aus mehreren "C"-Funktionen (im Gegensatz zu HAL-Funktionen):

int kinematicsForward(const double *joint, EmcPose *world,
const KINEMATICS_FORWARD_FLAGS *fflags,
KINEMATICS_INVERSE_FLAGS *iflags)

Implementiert die forward kinematics function.

int kinematicsInverse(const EmcPose * world, double *joints,
const KINEMATICS_INVERSE_FLAGS *iflags,
KINEMATICS_FORWARD_FLAGS *fflags)

Implementiert die Funktion der inversen Kinematik.

KINEMATICS_TYPE kinematicsType(void)

Gibt die Kennung des Kinematik-Typs zurück, typischerweise KINEMATICS_BOTH:

  1. KINEMATICS_IDENTITY (jede Gelenknummer entspricht einem Achsenbuchstaben)

  2. KINEMATICS_BOTH (Vorwärts- und Rückwärtskinematikfunktionen werden bereitgestellt)

  3. KINEMATICS_FORWARD_ONLY

  4. KINEMATICS_INVERSE_ONLY

Anmerkung
 GUIs können KINEMATICS_IDENTITY so interpretieren, dass die Unterscheidung zwischen Gelenknummern und Achsenbuchstaben im Gelenkmodus (typischerweise vor der Referenzfahrt) ausgeblendet wird. 
int kinematicsSwitchable(void)
int kinematicsSwitch(int switchkins_type)
KINS_NOT_SWITCHABLE

Die Funktion kinematicsSwitchable() gibt 1 zurück, wenn mehrere Kinematiktypen unterstützt werden. Die Funktion kinematicsSwitch() wählt den Kinematik-Typ aus. Siehe Switchable Kinematitcs.

Anmerkung
 Die meisten Kinematikmodule unterstützen einen einzigen Kinematiktyp und verwenden die Direktive "KINS_NOT_SWITCHABLE", um Standardwerte für die erforderlichen Funktionen kinematicsSwitchable() und kinematicsSwitch() zu liefern. 
int kinematicsHome(EmcPose *world, double *joint,
KINEMATICS_FORWARD_FLAGS *fflags,
KINEMATICS_INVERSE_FLAGS *iflags)

Die Funktion home kinematics setzt alle ihre Argumente auf ihre richtigen Werte an der bekannten Ausgangsposition. Beim Aufruf sollten diese, sofern bekannt, auf Anfangswerte, z.B. aus einer INI-Datei, gesetzt werden. Wenn die Home-Kinematik beliebige Startpunkte akzeptieren kann, sollten diese Anfangswerte verwendet werden.

int rtapi_app_main(void)
void rtapi_app_exit(void)

Dies sind die Standardfunktionen zum Auf- und Abbauen von RTAPI-Modulen.

Wenn sie in einer einzigen Quelldatei enthalten sind, können Kinematikmodule mit halcompile kompiliert und installiert werden. Weitere Informationen finden Sie in der Manpage halcompile(1) oder im HAL-Handbuch.

4.1. Kinematikmodul unter Verwendung der Vorlage userkins.comp

Eine weitere Möglichkeit, ein benutzerdefiniertes Kinematikmodul zu erstellen, ist die Anpassung der HAL Komponente userkins. Diese Vorlagenkomponente kann von einem Benutzer lokal geändert und mit halcompile erstellt werden.

Weitere Informationen finden Sie in den Man Pages von userkins.

Beachten Sie, dass zur Erstellung von schaltbaren kinematischen Modulen die erforderlichen Änderungen etwas komplizierter sind.

Siehe millturn.comp als Beispiel für ein umschaltbares kinematisches Modul, das mit der Vorlage userkins.comp erstellt wurde.