 Figure: PID Loop
Figure: PID LoopBASE_PERIOD is the "heartbeat" of your EMC computer. Every period, the software step generator decides if it is time for another step pulse. A shorter period will allow you to generate more pulses per second, within limits. But if you go too short, your computer will spend so much time generating step pulses that everything else will slow to a crawl, or maybe even lock up. Latency and stepper drive requirements affect the shortest period you can use.
Worst case latencies might only happen a few times a minute, and the odds of bad latency happening just as the motor is changing direction are low. So you can get very rare errors that ruin a part every once in a while and are impossible to troubleshoot.
The simplest way to avoid this problem is to choose a BASE_PERIOD that is the sum of the longest timing requirement of your drive, and the worst case latency of your computer. This is not always the best choice for example if you are running a drive with a 20uS hold time requirement, and your latency test said you have a maximum latency of 11uS, then if you set the BASE_PERIOD to 20+11 = 31uS and a not-so-nice 16,129 steps per second.
The problem is with the 20uS hold time requirement. That plus the 11uS latency is what forces us to use a slow 31uS period. But the EMC2 software step generator has some parameters that let you increase the various time from one period to several. For example, if steplen is changed from 1 to 2, then it there will be two periods between the beginning and end of the step pulse. Likewise, if dirhold is changed from 1 to 3, there will be at least three periods between the step pulse and a change of the direction pin.
If we can use dirhold to meet the 20uS hold time requirement, then the next longest time is the 4.5uS high time. Add the 11uS latency to the 4.5uS high time, and you get a minimum period of 15.5uS. When you try 15.5uS, you find that the computer is sluggish, so you settle on 16uS. If we leave dirhold at 1 (the default), then the minimum time between step and direction is the 16uS period minus the 11uS latency = 5uS, which is not enough. We need another 15uS. Since the period is 16uS, we need one more period. So we change dirhold from 1 to 2. Now the minimum time from the end of the step pulse to the changing direction pin is 5+16=21uS, and we don't have to worry about the drive stepping the wrong direction because of latency.
For more information on stepgen see Section ([->]).
Step Timing and Step Space on some drives are different. In this case the Step point becomes important. If the drive steps on the falling edge then the output pin should be inverted.
Servo systems must be "tuned" as they don't quite work out of the box like a stepper system might. This is because servos don't "step" in fixed increments like steppers do. PID is the "Black Magic" that makes your servos move where you want them to move and when you want them to move.
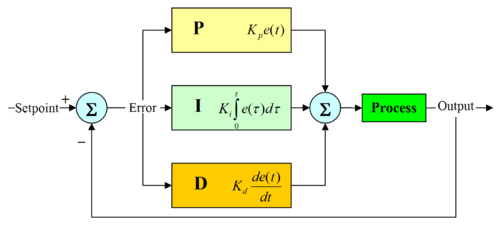
PID stand for Proportional, Integral, and Derivative. The Proportional value determines the reaction to the current error, the Integral value determines the reaction based on the sum of recent errors, and the Derivative value determines the reaction based on the rate at which the error has been changing. They are three common mathematical techniques that are applied to the task of getting a working process to follow a set point. In the case of EMC the process we want to control is actual axis position and the set point is the commanded axis position.
 Figure: PID Loop
Figure: PID LoopBy "tuning" the three constants in the PID controller algorithm, the controller can provide control action designed for specific process requirements. The response of the controller can be described in terms of the responsiveness of the controller to an error, the degree to which the controller overshoots the set point and the degree of system oscillation.
The proportional term (sometimes called gain) makes a change to the output that is proportional to the current error value. A high proportional gain results in a large change in the output for a given change in the error. If the proportional gain is too high, the system can become unstable. In contrast, a small gain results in a small output response to a large input error. If the proportional gain is too low, the control action may be too small when responding to system disturbances.
In the absence of disturbances, pure proportional control will not settle at its target value, but will retain a steady state error that is a function of the proportional gain and the process gain. Despite the steady-state offset, both tuning theory and industrial practice indicate that it is the proportional term that should contribute the bulk of the output change.
The contribution from the integral term (sometimes called reset) is proportional to both the magnitude of the error and the duration of the error. Summing the instantaneous error over time (integrating the error) gives the accumulated offset that should have been corrected previously. The accumulated error is then multiplied by the integral gain and added to the controller output.
The integral term (when added to the proportional term) accelerates the movement of the process towards set point and eliminates the residual steady-state error that occurs with a proportional only controller. However, since the integral term is responding to accumulated errors from the past, it can cause the present value to overshoot the set point value (cross over the set point and then create a deviation in the other direction).
The rate of change of the process error is calculated by determining the slope of the error over time (i.e. its first derivative with respect to time) and multiplying this rate of change by the derivative gain.
The derivative term slows the rate of change of the controller output and this effect is most noticeable close to the controller set point. Hence, derivative control is used to reduce the magnitude of the overshoot produced by the integral component and improve the combined controller-process stability.
If the PID controller parameters (the gains of the proportional, integral and derivative terms) are chosen incorrectly, the controlled process input can be unstable, i.e. its output diverges, with or without oscillation, and is limited only by saturation or mechanical breakage. Tuning a control loop is the adjustment of its control parameters (gain/proportional band, integral gain/reset, derivative gain/rate) to the optimum values for the desired control response.
A simple tuning method is to first set the I and D values to zero. Increase the P until the output of the loop oscillates, then the P should be set to be approximately half of that value for a "quarter amplitude decay" type response. Then increase I until any offset is correct in sufficient time for the process. However, too much I will cause instability. Finally, increase D, if required, until the loop is acceptably quick to reach its reference after a load disturbance. However, too much D will cause excessive response and overshoot. A fast PID loop tuning usually overshoots slightly to reach the set point more quickly; however, some systems cannot accept overshoot, in which case an "over-damped" closed-loop system is required, which will require a P setting significantly less than half that of the P setting causing oscillation.
The Real Time Application Interface (RTAI) is used to provide the best Real Time (RT) performance. The RTAI patched kernel lets you write applications with strict timing constraints. RTAI gives you the ability to have things like software step generation which require precise timing.
The Advanced Configuration and Power Interface (ACPI) has a lot of different functions, most of which interfere with RT performance (for example: power management, CPU power down, CPU frequency scaling, etc). The EMC2 kernel (and probably all RTAI-patched kernels) has ACPI disabled. ACPI also takes care of powering down the system after a shutdown has been started, and that's why you need to push the power button to completely turn off your computer.